使用ZEMAX 序列模式模拟激光二极管光源
发布时间:
半导体激光器又称激光二极管,是用半导体材料作为工作物质的激光器。半导体二极管激光器是最实用最重要的一类激光器。它体积小、寿命长,并可采用简单的注入电流的方式来泵浦其工作电压和电流与集成电路兼容,因而可与之单片集成。并且还可以用高达GHz的频率直接进行电流调制以获得高速调制的激光输出。由于这些优点,半导体二极管激光器在激光通信、光存储、光陀螺、激光打印、测距以及雷达等方面以及获得了广泛的应用。工业激光设备上用的半导体激光器一般为1064nm、532nm、355nm,功率从几瓦到几千瓦不等。一般在SMT模板切割、汽车钣金切割、激光打标机上使用的是1064nm的,532nm适用于陶瓷加工、玻璃加工等领域,355nm紫外激光适用于覆盖膜开窗、FPC切割、硅片切割与划线、高频微波电路板加工等领域。军事领域半导体激光器应用于如激光制导跟踪、激光雷达、激光引信、光测距、激光通信电源、激光模拟武器、激光瞄准告警、激光通信和激光陀螺等。
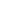
半导体激光二极管基本结构:垂直于PN结面的一对平行平面构成法布里—珀罗谐振腔,它们可以是半导体晶体的解理面,也可以是经过抛光的平面。其余两侧面则相对粗糙,用以消除主方向外其他方向的激光作用。激光二极管由于PN结发光位置不同,形成了两个方向的发散角,称之为二极管的快轴和慢轴如图所示,平行于PN结的方向为慢轴方向,垂直于PN结的方向为快轴方向,对于发光角度来说,快轴的发散角要大于慢轴发散角,一般两者的比值在2-3倍左右。
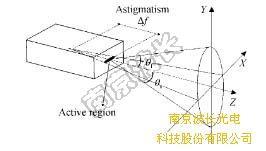
公式如下:
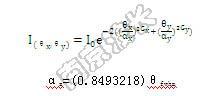
公式中:θx和θy是快轴和慢轴的发散角,Gx和Gy是X和Y方向光束的超高斯因子,用来控制二极管光源能量的集中度。若Gx=Gy=1时则为理想高斯光束。αx或αy 是光束发散角大小,用来计算激光半功率远场发散全角度因子。通常二极管厂家会给出激光功率衰减至一半时的半宽角度即θFWHM,也称为半功率角。对于高斯光束,光束半径通常定义为处于峰值强度的 1/e2处对应的半径。半功率角是由高斯光束半径确定的半发散角的1.18倍。
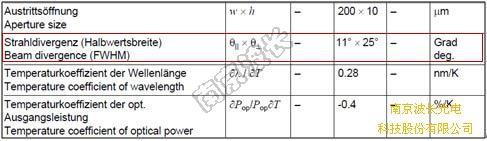
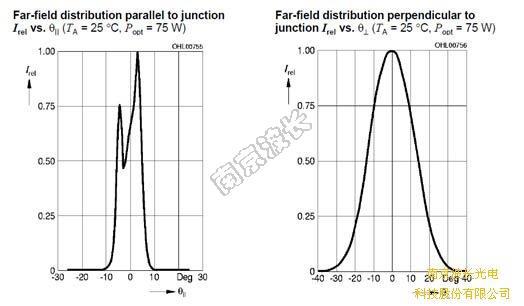
图1 OSRAM-SPL PL903 二极管参数表及半功率角图示
一般我们在ZEMAX中使用非序列模式来模拟激光二极管光源,方法较方便快捷。而当遇到较复杂系统运用或要求较高或光路优化时,需要在序列模式下模拟出激光二极管光源,此时光源模拟就较为复杂。
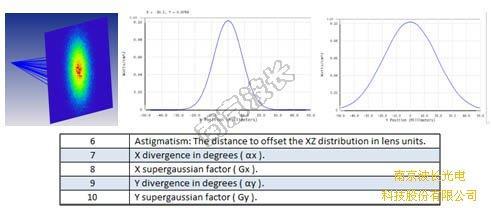
上图为激光二极管在非序列模式下光源的模拟,可见到出射为椭圆形光斑。其中设置选项Astigmatism,它是像散因子,即光束在X轴方向漂移的大小,当设置此参数时,说明二极管不是理想的点发出的。
序列模式中模拟激光二极管
方法一、利用理想圆柱透镜 (Paraxial XY) 的设置,加上点光源来完成。
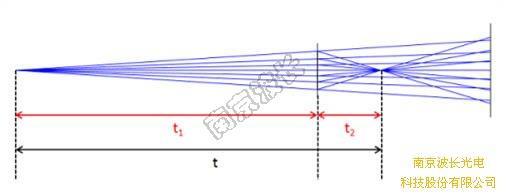
图3 光路示意图
步骤:1设定:光源在XZ面上的半功率角为θ∥。⊥∥
YZ面上的半功率角为θ⊥。
Astigmatism长度为t。
2. 光源在XZ面上的半功率角的发散角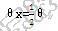
YZ面上的半功率角的发散角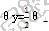
使用下面公式计算M(放大率)、t1、t2、φy(光焦度):
M = tanθx / tanθy
t1 = t / (M+1)
t2 = Mt / (M+1)
φy = (M+1)^2 / Mt
3. 设定System Explorer 的Aperture型态为「Object Space NA」,并且输入数值sin(θx)。
4. 物面到第一面的距离设为t1。
5. 把第一面设为光栏面,并设定面型态为 Paraxial XY:X Power = 0、Y Power = φy。
6. 以上的设定即可表现光源的部分。X方向的发光点是在第0面,而Y方向的发光点是在第一面开始t2的位置上。
范例:设定,假设LD规格如下:
θx = 5.5°
θy= 12.5°
t = 0.1 mm
依据上述公式计算后,得到:
M = 0.43
t1 = 0.0699
t2 = 0.3
φy = 47.556
在System Explorer中设定如下:
* Object Space NA = n sin(θx)=0.0958
* Apodization Type = Gaussian
* Apodization Factor = 0.3466
在Apodization Factor的地方输入0.3466,是因为这样在Aperture最边缘处,也就是NA=0.0958的位置,强度会刚好是二分之一。
讨论:
高斯光束 的剖面光强度分布:
其中,为束腰,r为光束的径向坐标,高斯光束的边缘(r=)定义为强度为中心强度的.
The amplitude at other points in the entrance pupil is given by:
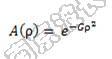
G is the apodization factor and ρ is the normalized pupil coordinate.
注意,此时是振幅的表达,如变换成强度,需要振幅的平方。
现要使得apodization光线边缘为中间强度的一半(r=)。则公式计算如下:
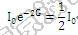
得到G=0.3465.
在Lens Data 中最后一面至像面的距离为100,模拟远场情况。

图4 Lens Data设置
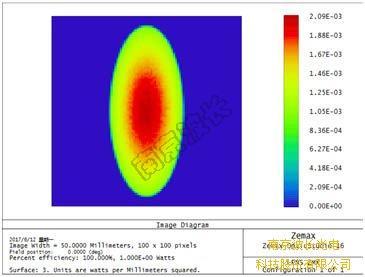
图5 远场照度图
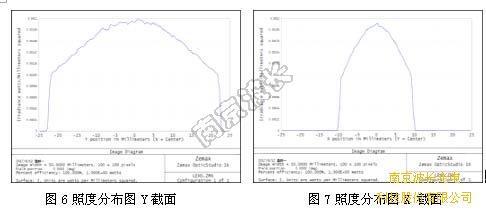
照度分布图的Y节面 (Cross Y)。离光源100mm时,Y = 22.17mm时照度值大约降为一半。换算过来大约是θy= 12.5°,即θ⊥= 25°。
照度分布图的X方向(Cross X)。离光源100mm处,X = 9.6mm的照度值大约降为一半。换算过来大约是θx = 5.5°,即θ∥=11°。
方法二:单纯使用Vignetting Factor来模拟。
存在很多关于发散角的定量定义: 1最常用的定义是,光束发散角为光束半径对远场轴向位置的导数,也就是与束腰的距离远大于瑞利长度。这一定义延伸出发散角概念(单位为弧度),依赖于光束半径的定义。对于高斯光束,光束半径通常定义为处于峰值强度的 1/e2处对应的半径。而非高斯形状的光束,可以采用积分公式。2除了在高斯光束中取处于 1/e2峰值强度处对应的点的角度作为发散角之外,还可以采用半高全宽(FWHM)发散角。在激光二极管和发光二极管数据表格中通常采用。高斯光束中,采用这种定义的发散角是由高斯光束半径确定的发散角的1.18倍。
举个例子,小的边发射激光二极管快轴对应的FWHM光束发散角为30°。这对应1/e2光束发散角为25.4°,很显然为了在不截断它的情况下使这一光束准直需要采用相当大数值孔径的棱镜。很大发散的光束需要采用一些光学装置以避免球面像差引起的光束质量下降。
设定 假设LD规格如下:
θ∥ = 11°
θ⊥= 25°
高斯函数强度一半时的 “全角 (也就是2FWHM)” 与强度为1/e^2时的 “半角” 的比值之计算方法如下:
α= 0.8493218 * FWHM
因此:
X方向的1/e^2强度的发散角角为11° ×0.85 = 9.35°
Y方向的1/e^2强度的发散角为25° ×0.85 = 21.25°
因为Vignetting Factor是在入瞳坐标上定义的,需计算光束投影到平面上时,半径的比值:
tan(9.35°) = 0.1647
tan(21.25°) = 0.3889
0.1647 / 0.3889 = 0.4235
因此如果在Vignetting Factor中输入VCX = 0.5765,就可以产生一个0.4235:1的椭圆形光束。
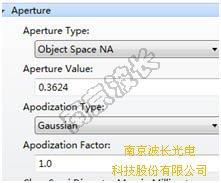
现在请在System Explorer > Aperture中输入如下的Object Space NA=sin(21.25°)=0.3624,并设定Gaussian Apodization以及Apodization Factor = 1。
在System Explorer > Field中输入如下的Vignetting Factor:

图9 视场中渐晕因子设置
在Lens Data Editor中输入如下数据。
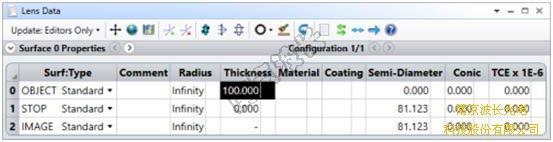
图10 Lens Data 设置
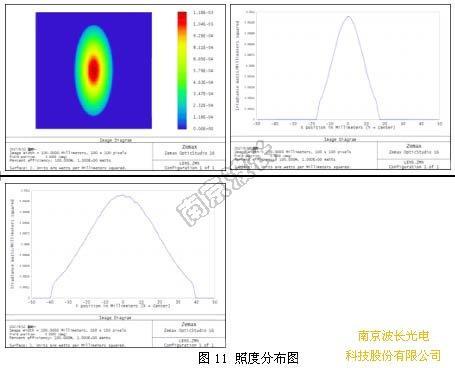
让我们确认看看距离光源100 mm的位置的照度吧。
copyright © 2022 开云手机版官方登录